13. Siamese Networks [Andrei Bursuc]

.center.footer[Marc LELARGE and Andrei BURSUC | Deep Learning Do It Yourself | 13. Siamese Networks]

---

# 13. Siamese Networks and Representation Learning

url: https://dataflowr.github.io/website/

.citation[
With slides from F. Fleuret, O. Grisel, E. Oyallon, G. Louppe, Y. Avrithis ...]

---

# Siamese networks

.center.width-60[![](images/part13/lfw.png)]

- **Recognition:** given a face, classify among K possible persons
- **Verification:** verify that two faces belongs to the same person

A verification system can be implemented as a similarity measure. If it's really good, useful for recognition.

---

.hidden.big[In addition, for such use-cases, new classes can appear on the fly anytime.]

---

---

.big[Instead of training a network to do classification, we can train it to compute useful features from images, allowing us to measure similarities/dissimilarities between images.]

---

# Siamese architecture

.center.width-60[![](images/part13/siamese_1.png)]

- an input sample is a _pair_ $( \mathbf{x}\_i, \mathbf{x}\_j)$

.citation[ S. Chopra et al.,Learning a similarity metric discriminatively, with application to face verification, CVPR 2005]
---

# Siamese architecture

.center.width-60[![](images/part13/siamese_2.png)]

- an input sample is a _pair_ $( \mathbf{x}\_i, \mathbf{x}\_j)$
- both $\mathbf{x}\_i$, $\mathbf{x}\_j$ go through the _same_ function $f$ with _shared_ parameters $\theta$

.citation[ S. Chopra et al.,Learning a similarity metric discriminatively, with application to face verification, CVPR 2005]

---

# Siamese architecture

.center.width-60[![](images/part13/siamese_3.png)]

- an input sample is a _pair_ $( \mathbf{x}\_i, \mathbf{x}\_j)$
- both $\mathbf{x}\_i$, $\mathbf{x}\_j$ go through the _same_ function $f$ with _shared_ parameters $\theta$
- loss $\ell\_{ij}$ is measured on output pair $( \mathbf{y}\_i, \mathbf{y}\_j)$ and target $t\_{ij}$

.citation[ S. Chopra et al.,Learning a similarity metric discriminatively, with application to face verification, CVPR 2005]
---

# Contrastive loss

.center.width-60[![](images/part13/contrastive_1.png)]

- input samples $\mathbf{x}\_i$, output vectors $\mathbf{y}\_i= f(\mathbf{x}\_i; \theta)$, target variables $t\_{ij}=\mathbb{1}[\text{sim}(\mathbf{x}\_i, \mathbf{x}\_j)]$
- _contrastive loss_ is a function of distance $\Vert \mathbf{y}\_i - \mathbf{y}\_j \Vert$ only 
 
 $$\ell\_{ij} = L((\mathbf{y}\_i,\mathbf{y}\_j), t\_{ij} ) = \ell (\Vert \mathbf{y}\_i - \mathbf{y}\_j \Vert,  t\_{ij})$$

.citation[ R. Hadsell et al., Dimensionality reduction by learning an invariant mapping, CVPR 2006]
---

# Contrastive loss

.center.width-60[![](images/part13/contrastive_2.png)]

- _similar_ samples are _attracted_

$$\ell(x,t)=\textcolor{red}{t\ell^{+}} + (1-t)\ell^{-}(x) = \textcolor{red}{t x^2} + (1-t)[m-x]^2\_+$$

---

# Contrastive loss

.center.width-60[![](images/part13/contrastive_3.png)]

- _dissimilar_ samples are _repelled_ if closer than margin $m$

$$\ell(x,t)=t\ell^{+} + (1-t)\textcolor{red}{\ell^{-}(x)} = t x^2 + (1-t)\textcolor{red}{[m-x]^2\_+}$$

---

# Training siamese networks

## Data collection and loading
- sample positive pairs $( \mathbf{x}\_i, \mathbf{x}\_j)$, with samples coming from the same class
- sample negative pairs $( \mathbf{x}\_i, \mathbf{x}\_j)$, with samples of different classes
- combine pairs of samples in larger mini-batches
- __it's highly important to properly tune mini-batches__: balance positives and negatives, discard easy negatives and positives and focus on more difficult ones.

.hidden[
## Learning
- pass all images through the two networks with shared parameters (in fact the same network)
- backpropagate through the two networks and sum gradients from the two samples
]

---
count: false
# Training siamese networks

## Learning
- pass all images through the two networks with shared parameters (in fact the same network)
- backpropagate through the two networks and sum gradients from the two samples

---

# Triplet architecture

.grid[
.kol-6-12[
.center.width-100[![](images/part13/triplet_1.png)]
]
.kol-6-12[
- an input sample is a _triple_ $(\mathbf{x}\_i, \mathbf{x}\_i^+, \mathbf{x}\_i^-)$
]
]
.citation[ Wang et al., Learning fine-grained image similarity with deep ranking, CVPR 2014]
---

# Triplet architecture

- an input sample is a _triple_ $(\mathbf{x}\_i, \mathbf{x}\_i^+, \mathbf{x}\_i^-)$
- $\mathbf{x}\_i, \mathbf{x}\_i^+, \mathbf{x}\_i^-$ go through the _same_ function $f$ with _shared_ parameters $\theta$
]
]
.citation[ Wang et al., Learning fine-grained image similarity with deep ranking, CVPR 2014]
---

# Triplet architecture

- an input sample is a _triple_ $(\mathbf{x}\_i, \mathbf{x}\_i^+, \mathbf{x}\_i^-)$
- $\mathbf{x}\_i, \mathbf{x}\_i^+, \mathbf{x}\_i^-$ go through the _same_ function $f$ with _shared_ parameters $\theta$
- loss $\ell\_i$ is measured on output triple $(\mathbf{y}\_i, \mathbf{y}\_i^+, \mathbf{y}\_i^-)$ 
]
]
.citation[ Wang et al., Learning fine-grained image similarity with deep ranking, CVPR 2014]

---
# Triplet loss

- input _anchor_ $\mathbf{x}\_i$, output $\mathbf{y}\_i = f(\mathbf{x}\_i; \theta)$; positive $\mathbf{y}\_i^+ = f(\mathbf{x}\_i^+; \theta)$, negative $\mathbf{y}\_i^- = f(\mathbf{x}\_i^-; \theta)$ 
- _triplet loss_ is a function of distances $\Vert \mathbf{y}\_i - \mathbf{y}\_i^+ \Vert$, $\Vert \mathbf{y}\_i - \mathbf{y}\_i^- \Vert$ only

$$\ell\_i = L(\mathbf{y}\_i, \mathbf{y}\_i^+, \mathbf{y}\_i^-) =\ell(\Vert \mathbf{y}\_i - \mathbf{y}\_i^+ \Vert, \Vert \mathbf{y}\_i - \mathbf{y}\_i^- \Vert)$$

$$\ell(x^+, x^-) = [m + (x^+)^2 - (x^-)^2]\_+$$

so distance $\Vert \mathbf{y}\_i - \mathbf{y}\_i^+ \Vert$ should be less than $\Vert \mathbf{y}\_i - \mathbf{y}\_i^- \Vert$ by _margin_ $m$

---
# Triplet loss

$$\ell\_i = L(\mathbf{y}\_i, \mathbf{y}\_i^+, \mathbf{y}\_i^-) =\ell(\Vert \mathbf{y}\_i - \mathbf{y}\_i^+ \Vert, \Vert \mathbf{y}\_i - \mathbf{y}\_i^- \Vert)$$

$$\ell(x^+, x^-) = [m + (x^+)^2 - (x^-)^2]\_+$$

so distance $\Vert \mathbf{y}\_i - \mathbf{y}\_i^+ \Vert$ should be less than $\Vert \mathbf{y}\_i - \mathbf{y}\_i^- \Vert$ by _margin_ $m$

- by taking _two pairs_ $(\mathbf{x}\_i, \mathbf{x}\_i^+)$ and $(\mathbf{x}\_i, \mathbf{x}\_i^-)$ at a time with targets $1$, $0$ respectively, the _contrastive loss_ can be writen similarly
$$\ell(x^+, x^-) = (x^+)^2 + [m-x^-]^2\_+$$
so distance $\Vert \mathbf{y}\_i - \mathbf{y}\_i^+ \Vert$ should be small and $\Vert \mathbf{y}\_i - \mathbf{y}\_i^- \Vert$ larger than $m$

---
count: false
# Training with the triplet loss

$$\ell\_i = L(\mathbf{y}\_i, \mathbf{y}\_i^+, \mathbf{y}\_i^-) =\ell(\Vert \mathbf{y}\_i - \mathbf{y}\_i^+ \Vert, \Vert \mathbf{y}\_i - \mathbf{y}\_i^- \Vert)$$

- sample a mini-batch of triplets$(\mathbf{x}\_i, \mathbf{x}\_i^+, \mathbf{x}\_i^-)$
- forward pass on all $3$ networks
- compute loss over all samples and sum gradients for updating weights

---

# Siamese networks

```
class SiameseNet(nn.Module):
    def __init__(self, embedding_net):
        super(SiameseNet, self).__init__()
        self.embedding_net = embedding_net

def forward(self, x1, x2):
        output1 = self.embedding_net(x1)
        output2 = self.embedding_net(x2)
        return output1, output2

def get_embedding(self, x):
        return self.embedding_net(x)
```
]

```
class TripletNet(nn.Module):
    def __init__(self, embedding_net):
        super(TripletNet, self).__init__()
        self.embedding_net = embedding_net

def forward(self, x1, x2, x3):
        output1 = self.embedding_net(x1)
        output2 = self.embedding_net(x2)
        output3 = self.embedding_net(x3)
        return output1, output2, output3

def get_embedding(self, x):
        return self.embedding_net(x)
```
]
]
---

count:false

# Siamese networks

```
class SiameseNet(nn.Module):
    def __init__(self, embedding_net):
        super(SiameseNet, self).__init__()
        self.embedding_net = embedding_net

def forward(self, x1, x2):
*       output1 = self.embedding_net(x1)
*       output2 = self.embedding_net(x2)
        return output1, output2

def get_embedding(self, x):
        return self.embedding_net(x)
```
]

```
class TripletNet(nn.Module):
    def __init__(self, embedding_net):
        super(TripletNet, self).__init__()
        self.embedding_net = embedding_net

def forward(self, x1, x2, x3):
*       output1 = self.embedding_net(x1)
*       output2 = self.embedding_net(x2)
*       output3 = self.embedding_net(x3)
        return output1, output2, output3

def get_embedding(self, x):
        return self.embedding_net(x)
```
]
]

---

# Hard negative sampling

After a few epochs, If $(\mathbf{x}\_i, \mathbf{x}\_i^{+}, \mathbf{x}\_i^{-})$ are chosen randomly, it will be easy to satisfy the inequality in the loss.

Gradients in one batch quickly become almost $0$ except for **hard cases**.
Random sampling is inefficient to find these hard cases

--
count: false

- **Hard triplet sampling:** sample $\mathbf{x}\_i^{-}$ such that:

$$||\mathbf{y} - \mathbf{y}^{+}|| > ||\mathbf{y} - \mathbf{y}^{-}|| + m$$

- **Semi Hard triplet sampling:** sample $\mathbf{x}\_i^{-}$ such that:

$$||\mathbf{y} - \mathbf{y}^{+}|| > ||\mathbf{y} - \mathbf{y}^{-}||$$

---

# Applications

---

# Face recognition

.center.width-25[![](images/part13/facenet.png)]
- A threshold is computed on test set to decide which faces are the same
- Best model achieves 99.6% verification accuracy on Labeled Faces in the Wild dataset
- Works well even with non-camera facing faces

.citation[F. Schroff et al., Facenet: A unified embedding for face recognition and clustering, CVPR 2015 ]

---

# Deep image retrieval

.center.width-70[![](images/part13/dir_1.png)]

.citation[A. Gordo et al., Deep Image Retrieval: Learning Global Representations for Image Search, ECCV 2016 ]

- query $\mathbf{x}\_i$, relevant $\mathbf{x}\_i^+$ (same building), irrelevant $\mathbf{x}\_i^-$ (other building)

---
count: false
# Deep image retrieval

.center.width-70[![](images/part13/dir_2.png)]

.citation[A. Gordo et al., Deep Image Retrieval: Learning Global Representations for Image Search, ECCV 2016 ]

- query $\mathbf{x}\_i$, relevant $\mathbf{x}\_i^+$ (same building), irrelevant $\mathbf{x}\_i^-$ (other building)

---

.center.width-70[![](images/part13/dir_3.png)]

.citation[A. Gordo et al., Deep Image Retrieval: Learning Global Representations for Image Search, ECCV 2016 ]

- query $\mathbf{x}\_i$, relevant $\mathbf{x}\_i^+$ (same building), irrelevant $\mathbf{x}\_i^-$ (other building)
- triplet loss is evaluated on output $(\mathbf{y}\_i, \mathbf{y}\_i^+, \mathbf{y}\_i^-)$

---

# Patch matching

.center.width-45[![](images/part13/phototour.png)]

---

# Patch matching

.center.width-70[![](images/part13/local_descriptors_2.png)]

# Patch matching

.center.width-60[![](images/part13/local_descriptors_8.png)]

# Image reconstruction

.center.width-70[![](images/part13/sfm.png)]
.caption[Structure from motion]

.citation[F. Radenovic et al., CNN Image Retrieval Learns From BoW: Unsupervised Fine-Tuning with Hard Examples, ECCV 2016 
 Schonberger et al., From Single Image Query to Detailed 3D Reconstruction, CVPR 2015.]

---

# Person re-identification

]
.kol-6-12[
]
]

.citation[J. Almazan et al., Re-ID Done Right: towards Good Practices for Person re-Identification, arXiv 2018]

---

# Person re-identification

]
.kol-6-12[
.center.width-70[![](images/part13/reid2.png)]
]
]

.citation[J. Almazan et al., Re-ID Done Right: towards Good Practices for Person re-Identification, arXiv 2018]

---

---

# N-pair loss

.center.width-70[![](images/part13/n-pair-loss.png)]
.caption[Deep metric learning with (left) triplet loss and (right) $(N+1)$-tuplet loss. $(N+1)$-tuplet loss pushes $N-1$ negative examples all at once.]

- generalize *triplet-loss* with **N-pair loss**
- sample pairs of similar examples and use as negative all the other samples in the mini-batch

.citation[K. Sohn,  Improved Deep Metric Learning with Multi-class N-pair Loss Objective, NeurIPS 2016]

---
## Exemplar networks

.center.bigger.blue[The image on the left is a distorted crop extracted from an image, which of these crops has the same source image?]
.hidden.center.bigger.red[Easy if robust to the desired transformations (geometry and colour) ]

.grid[
.kol-4-12[
 
.center.width-25[![](images/part13/exemplar_1.png)]
]
.kol-8-12[
.center.width-100[![](images/part13/exemplar_2.png)]
]
]

.citation[A. Dosovitskiy et al., Discriminative Unsupervised Feature Learning with Exemplar Convolutional Neural Networks, PAMI 2015]

---
count: false
## Exemplar networks

.center.bigger.blue[The image on the left is a distorted crop extracted from an image, which of these crops has the same source image?]
.center.bigger.red[Easy if robust to the desired transformations (geometry and colour) ]

.grid[
.kol-4-12[
 
.center.width-25[![](images/part13/exemplar_1.png)]
]
.kol-8-12[
.center.width-100[![](images/part13/exemplar_3.png)]
]
]

.citation[A. Dosovitskiy et al., Discriminative Unsupervised Feature Learning with Exemplar Convolutional Neural Networks, PAMI 2015]

---
## Exemplar networks

.grid[
.kol-4-12[
.center.width-70[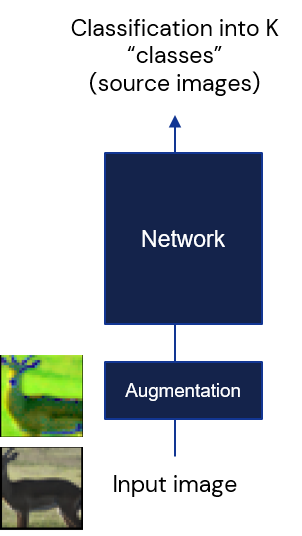![](images/part13/exemplar_4.png)]
]
.kol-8-12[
.bigger.green[Pros]
- Representations are invariant to desired transformations
- Requires preservation of fine-grained information

.bigger.red[Cons]
- Choosing the augmentations is important
- Exemplar based: images of the same class or instance are negatives
  - Nothing prevents it from focusing on the background
- Original formulation is not scalable (number of “classes” = dataset size)

]
]

.citation[A. Dosovitskiy et al., Discriminative Unsupervised Feature Learning with Exemplar Convolutional Neural Networks, PAMI 2015]

---

## Some notations

Let $\mathbf{x} \in \mathcal{X}$ be input data and $y \in \\{1, \dots, L\\}$ and $f\_{\theta}(\cdot):\mathcal{X}\rightarrow\mathbb{R}^D$ a network generating an embedding vector $f\_{\theta}(\mathbf{x})$.

We denote:
- $q=f\_{\theta}(\mathbf{x})$ (*query*)
- $\\{\mathbf{x}^{i}\\}$ a set of samples from $\mathcal{X}$.
- $k\_{i} = f\_{\theta}(\mathbf{x}^{i})$ the embeddings of $\\{\mathbf{x}^{i}\\}$ as keys (*representations*)

---
## Exemplar networks

.grid[
.kol-3-12[
.center.width-90[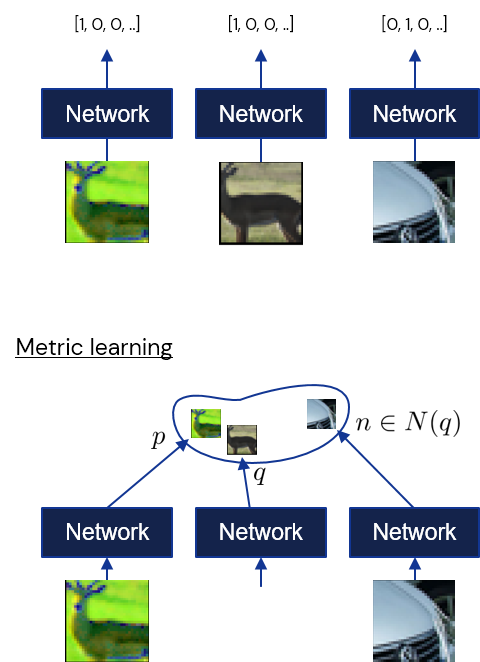![](images/part13/exemplar_5.png)]
]
.kol-9-12[
Exemplar ConvNets are not scalable (number of “classes” = number of training images)
- Using $w\_i$ as class prototype prevents explicit comparison between instances, i.e. individual samples
- We can use instead a _non-parametric_ variant that replaces $q^\top w\_j$ with $q^\top k\_i$

$$\mathcal{L}\_{\text{softmax}} (q, c(q)) = - \log\frac{\exp(q^\top w\_{c(q)})}{ \sum\_{c\in C}\exp(q^\top w\_{c})}$$
$$\downarrow$$
$$\mathcal{L}\_{\text{non-param-softmax}}(q) = - \log \frac{\exp(q^\top k\_q )}{ \sum\_{i \in N}\exp(q ^\top k\_{i})}$$

]
]

.citation[A. Dosovitskiy et al., Discriminative Unsupervised Feature Learning with Exemplar Convolutional Neural Networks, PAMI 2015]

---
count: false
## Exemplar networks

.grid[
.kol-3-12[
.center.width-90[![](images/part13/exemplar_5.png)]
]
.kol-9-12[
- $N$ is the number of training samples; $C$ is the number of classes 
- $c(q)$ is the class index of $q$
- $k\_q \in \\{ k\_i\\}$ is the key of a positive sample for $q$

]
]

.citation[A. Dosovitskiy et al., Discriminative Unsupervised Feature Learning with Exemplar Convolutional Neural Networks, PAMI 2015]

---

# Histogram loss

.center.width-70[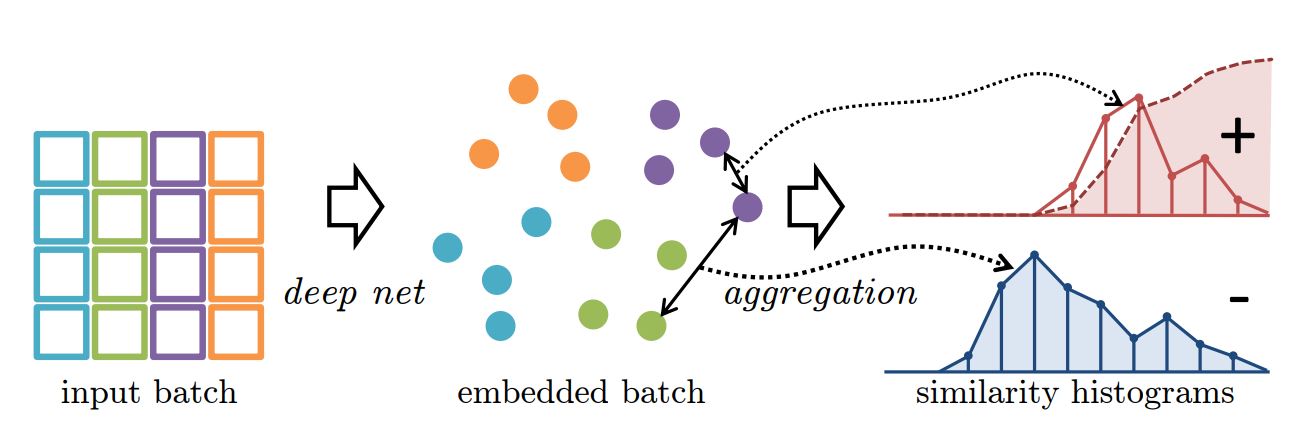![](images/part13/histogram-loss.jpg)]

- for a mini-batch compute all pairwise positive similarities and negative similarities

- compile similarities into distributions (differentiable approximations of distributions)

- the loss aims to repell the two distributions

---

## Few classes, few labels

---

# Prototypical networks

Learns to extract class prototype vectors:
- class prototype vector = mean feature vector of training examples
- classify test example to the class with the closest prototype ($L\_2$ distance)
- prototype vectors are similar to classification weights of networks

.kol-8-12[
Prototype vector of $k$-th class: $c\_k=\frac{1}{|S\_k|} \sum\_{(\mathbf{x}\_i, y\_i) \in S\_k} f\_{\theta}(\mathbf{x}\_i)$

Classification for example $x$:

$$p\_{\theta}(y=k|\mathbf{x}) = \frac{\exp(-d(f\_{\theta}(\mathbf{x}), c\_k))}{\sum\_{k'}\exp(-d(f\_{\theta}(\mathbf{x}), c\_{k'}))}$$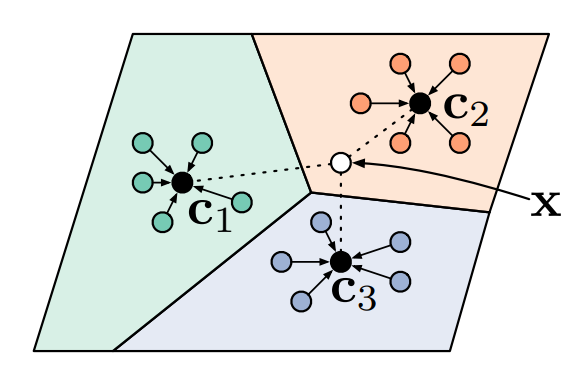
]

]

---

## Some classes with labels and some without labels

---

# Imprinting

The cosine classifier

$$p\_{\theta}(y=k|\mathbf{x}) = \frac{\exp(\tau f\_{\theta}(\mathbf{x})^\top w\_k  )} { \sum\_{k'}\exp(\tau f\_{\theta}(\mathbf{x})^\top w\_{k'}  )}$$

All vectors and weights are $L\_2$-normalized before the last layer

]
]

.citation[H. Qi et al., Low-Shot Learning with Imprinted Weights, CVPR 2018 S. Gidaris et al., Dynamic Few-Shot Visual Learning without Forgetting, CVPR 2018]

---

.kol-6-12[
.center.width-100[![](images/part13/imprinting_role.png)]
.caption[ _left_: before imprinting; _right_: after imprinting]
]
]

.citation[H. Qi et al., Low-Shot Learning with Imprinted Weights, CVPR 2018 S. Gidaris et al., Dynamic Few-Shot Visual Learning without Forgetting, CVPR 2018]
---

]

.kol-6-12[
- use network as feature extractor, train as usual
- for new class, compute average embedding vector
- use embedded vector as new class proxy/template
- can be also fine-tuned later on
]
]

.citation[H. Qi et al., Low-Shot Learning with Imprinted Weights, CVPR 2018 S. Gidaris et al., Dynamic Few-Shot Visual Learning without Forgetting, CVPR 2018]

---

# Imprinting

## Results

.kol-6-12[
.center[<img src="images/part13/imprinting_results3.png" style="width: 370px;" />]
]
.kol-6-12[
.center[<img src="images/part13/imprinting_results4.png" style="width: 370px;" />]
]
]

.citation[H. Qi et al., Low-Shot Learning with Imprinted Weights, CVPR 2018 S. Gidaris et al., Dynamic Few-Shot Visual Learning without Forgetting, CVPR 2018]

---
# Take-aways

- .big[A specific type of architectures suitable for representation learning]

- .big[In case of many classes and class imbalance, siamese networks might be better, while for standard settings use classification]

- .big[Modern methods leverage siamese networks for unsupervised learning, where the network must recognize a perturbed sample in a large pool of negatives.]

---

# Multi-modal siamese networks

---
# CLIP

.center.width-50[![](images/part13/clip-1.png)]

.center[Training an image network and a text network together from $400M$ pairs of images and captions crawled from Internet]

.citation[A. Radford et al., Learning Transferable Visual Models From Natural Language Supervision, arXiv 2021 ]

---
# CLIP

.center.width-55[![](images/part13/clip-2.png)]

.citation[A. Radford et al., Learning Transferable Visual Models From Natural Language Supervision, arXiv 2021 ]

---

## Implementation - numpy-like pseudocode

```python
# image_encoder - ResNet or Vision Transformer
# text_encoder - CBOW or Text Transformer
# I[n, h, w, c] - minibatch of aligned images
# T[n, l] - minibatch of aligned texts
# W_i[d_i, d_e] - learned proj of image to embed
# W_t[d_t, d_e] - learned proj of text to embed
# t - learned temperature parameter
# extract feature representations of each modality
I_f = image_encoder(I) #[n, d_i]
T_f = text_encoder(T) #[n, d_t]
# joint multimodal embedding [n, d_e]
I_e = l2_normalize(np.dot(I_f, W_i), axis=1)
T_e = l2_normalize(np.dot(T_f, W_t), axis=1)
# scaled pairwise cosine similarities [n, n]
logits = np.dot(I_e, T_e.T) * np.exp(t)
# symmetric loss function
labels = np.arange(n)
loss_i = cross_entropy_loss(logits, labels, axis=0)
loss_t = cross_entropy_loss(logits, labels, axis=1)
loss = (loss_i + loss_t)/2
```

.citation[A. Radford et al., Learning Transferable Visual Models From Natural Language Supervision, arXiv 2021 ]

---

## Works very well in practice

.center.width-40[![](images/part13/clip-3.png)]
.caption[Zero-shot CLIP is competitive with a fully supervised baseline]

.citation[A. Radford et al., Learning Transferable Visual Models From Natural Language Supervision, arXiv 2021 ]

---

Training CLIP is very expensive:
- ResNet (`RN50x64`): $18$ days on $592$ V100 GPUS
- ViT (Vision Transformer): $12$ days on $256$ V100 GPUs
- batch-size: $32.768$

Such models that are expensive to train but can be repurposed for other tasks, are referred to as *foundation models*.

---

# CLIPStyler

.center.width-65[![](images/part13/clipstyler-1.png)]

# CLIPStyler

.center.width-65[![](images/part13/clipstyler-2.png)]

---

# CLIPStyler

.center.width-75[![](images/part13/clipstyler-3.png)]
.center[Works similarly with image based styling]

---

# FlexIT

.center.width-90[![](images/part13/flexit-1.png)]
.center[Transform image using text indication]

---

# FlexIT

.center.width-90[![](images/part13/flexit-2.png)]
.center[Optimize latent variable only from a pre-trained generative model to steer it towards generativ what we want]

---

# Prompt-driven Zero-shot Domain Adaptation

.center.width-90[![](images/part13/lads-1.png)]
.center[Use textual information to generate features for domains we have seen yet]

.citation[Dunlap et al., Using Language to Extend to Unseen Domainsn, ICLR 2023 Fahes et al., PØDA: Prompt-driven Zero-shot Domain Adaptation, arXiv 2022]

---

# Prompt-driven Zero-shot Domain Adaptation

.center.width-90[![](images/part13/lads-2.png)]
.center[Use textual information to generate features for domains we have seen yet]

.citation[Dunlap et al., Using Language to Extend to Unseen Domainsn, ICLR 2023 Fahes et al., PØDA: Prompt-driven Zero-shot Domain Adaptation, arXiv 2022]

---

# Prompt-driven Zero-shot Domain Adaptation

.center.width-100[![](images/part13/poda-1.png)]
.center[Use textual information to generate features for domains we have seen yet]

.citation[Dunlap et al., Using Language to Extend to Unseen Domainsn, ICLR 2023 Fahes et al., PØDA: Prompt-driven Zero-shot Domain Adaptation, arXiv 2022]

---

# Stable Diffusion

.center.width-80[![](images/part13/stable-diffusion-1.png)]
.center[Condition image generation on text embeddings from CLIP]

---

# Stable Diffusion

.center.width-100[![](images/part13/stable-diffusion-2.png)]
.center[Text to image synthesis examples -- starting to very dated]

---

.bigger[CLIP is currently widely used in various computer vision and text tasks to kickstart or steer learning.]
.bigger[Intuitively the structured learned in the feature space from language can effectively steer visual representation more than simple individual labels.]

---

The end.